library(tidyverse)
set.seed(3124)
# 原始分布指数分布, 均值为1
data = tibble(x = rexp(10000, rate=1))
ggplot(data, aes(x)) +
geom_histogram(fill = "#4E84C4", color = "black") +
labs(title="原始总体分布(指数分布)", x="X", y="count")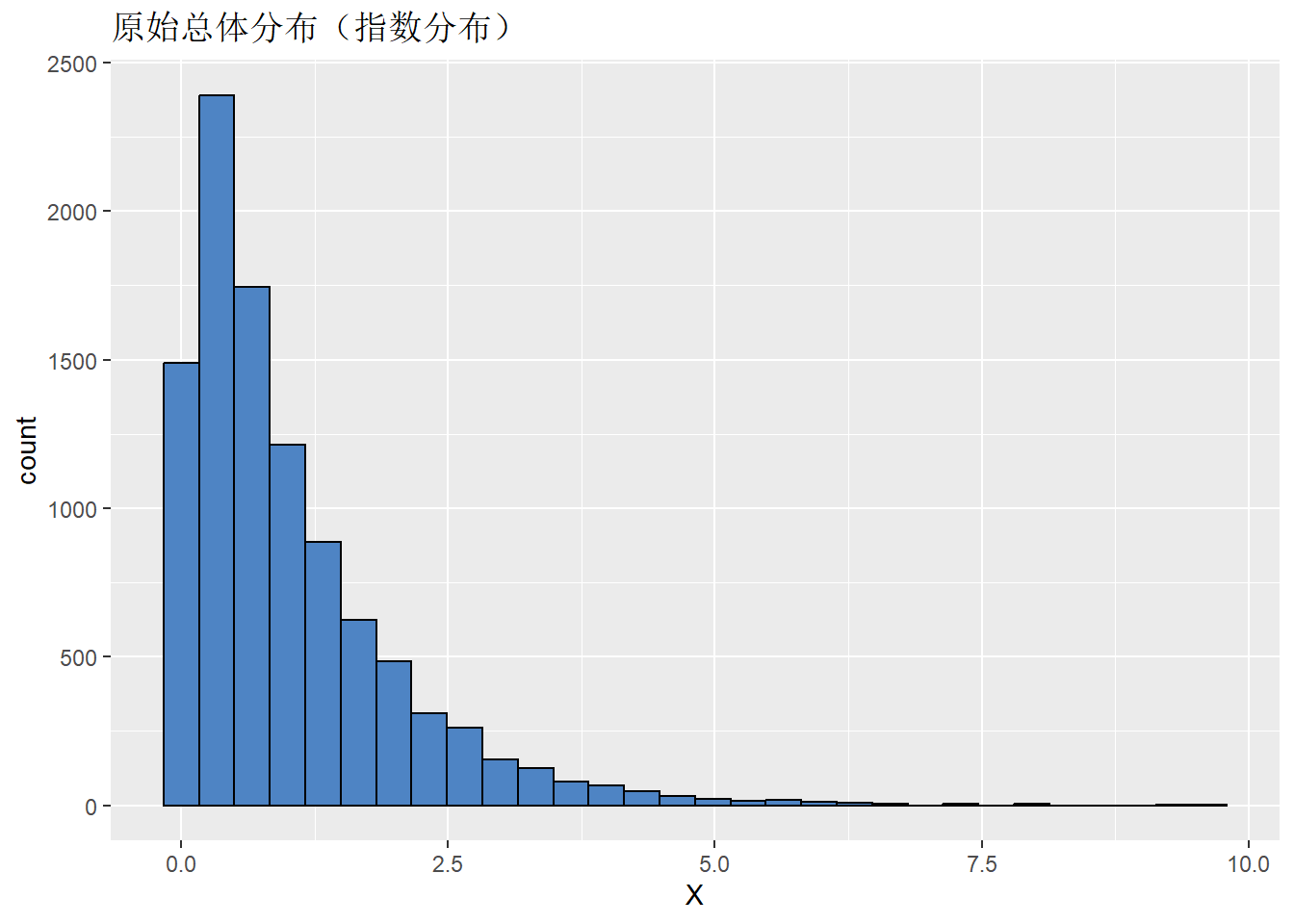
Pigking
March 15, 2025
中心极限定理: 对于任意分布(均值为\(\mu\), 方差为\(\sigma^2\)), 每次从总体中抽取n个样本, n足够大时(一般n>=30) 样本均值\(\overline{X}\)的分布近似服从\(N(\mu, \sigma^2/n)\), 即 \[ \begin{align*} \overline{X} \sim N(\mu,\sigma^2/n), \frac{\overline{X} - \mu}{\sigma / \sqrt{n}} \sim N(0,1) \end{align*} \] 下面是验证:
library(tidyverse)
set.seed(3124)
# 原始分布指数分布, 均值为1
data = tibble(x = rexp(10000, rate=1))
ggplot(data, aes(x)) +
geom_histogram(fill = "#4E84C4", color = "black") +
labs(title="原始总体分布(指数分布)", x="X", y="count")
# 每次抽样样本数
n = 100
# 不同抽样次数
sample_sizes = c(5, 10, 40, 100, 500, 1000)
results <- map_dfr(sample_sizes, ~ {
tibble(
sample_size = .x,
mean = map_dbl(1:.x, ~mean(sample_n(data, n)$x))
)
})
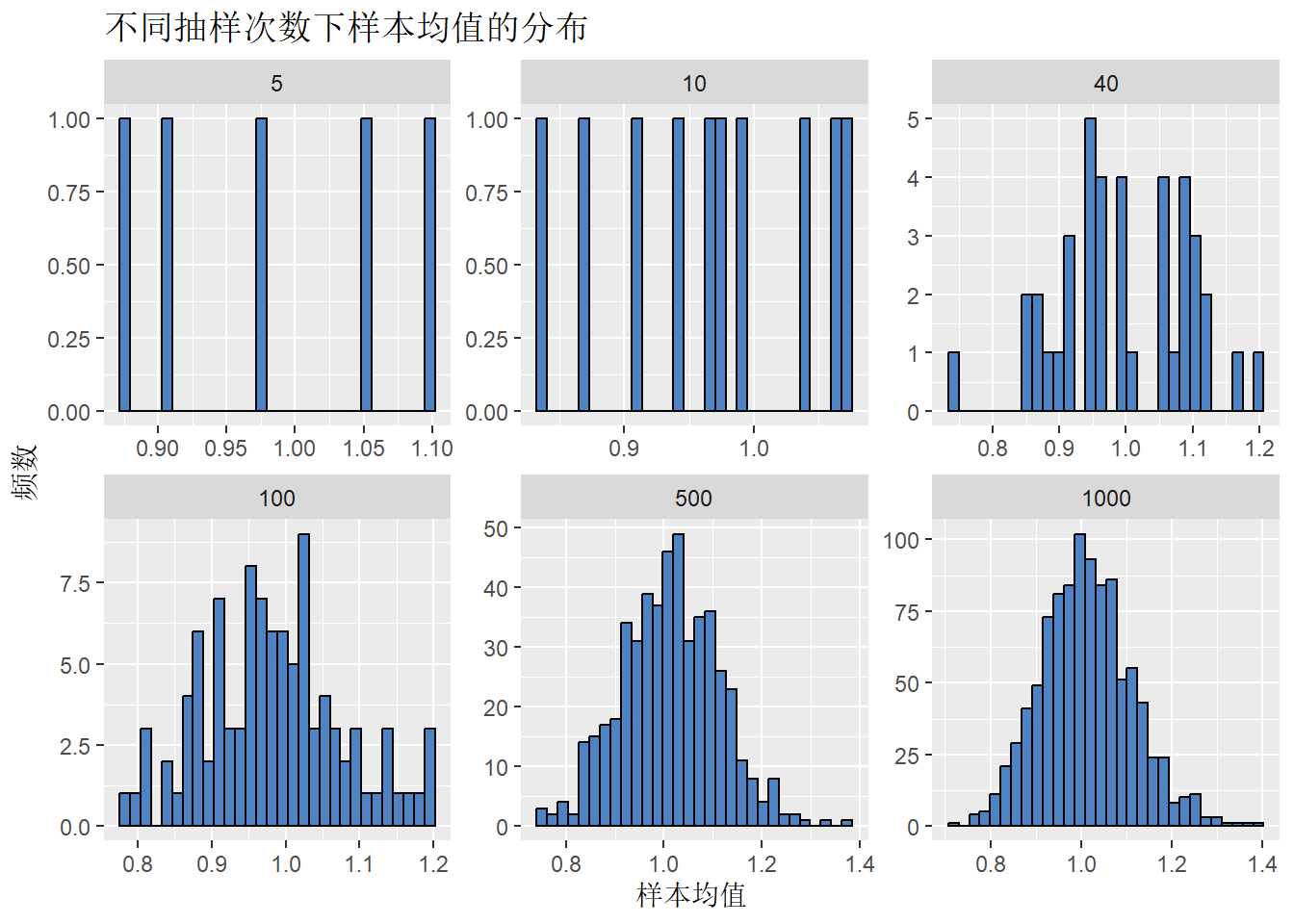
ggplot(results, aes(x = mean)) +
geom_histogram(fill = "#4E84C4", color = "black") +
facet_wrap(~ sample_size, scales = "free") +
labs(
title = "不同抽样次数下样本均值的分布",
x = "样本均值",
y = "频数"
) +
scale_color_brewer(palette = "Paired")